You may not realize it, but when you’ve tested a keyword or phrase, you can actually tell whether it works for you. It’s easy to do – just look at your site and imagine that the search term has been written above every word. If people are clicking on your page when they type that keyword into Google, then it’s probably working for you.
If you take a minute to think about how this affects your life, you’ll start to understand why this is so important. For example, let’s say you’re in the middle of a project and you need to find some extra resources. You decide to use an online resource to help you out, only to discover that you can’t find anything useful.
This isn’t because you haven’t searched hard enough. Instead, it could be because the search engine doesn’t even recognize the keyword you used. In other words, your search terms aren’t working for you.
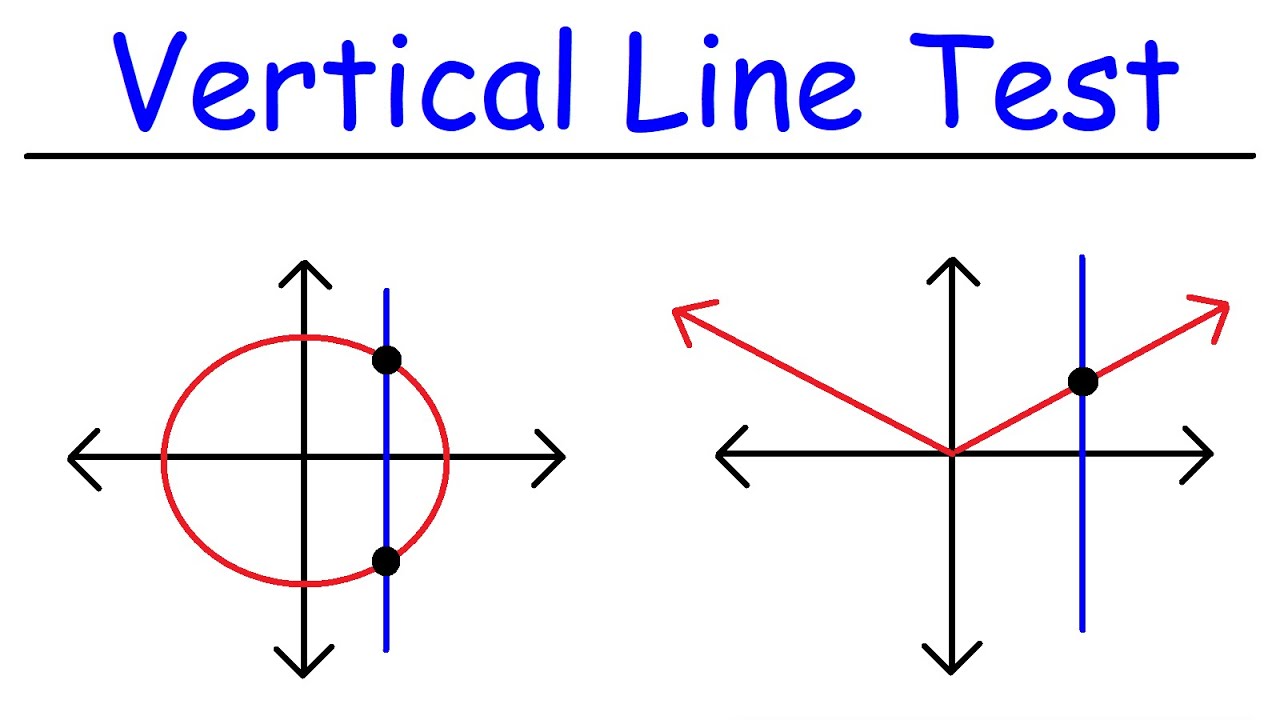
What is the Vertical Line Test?
All functions are equations, but not all equations are functions. Functions are equations that pass the Vertical Line Test. In other words, in order for a graph to be a function, no perfectly vertical line can cross its graph more than once.
When you draw vertical lines across your graph to test it, make sure that you draw your vertical lines perfectly straight.
The graph below doesn’t pass the Vertical Line Test, because a vertical line intersects it more than once. It takes only one vertical line intersecting the graph more than once for it to fail the Vertical Line Test.

Passing the Vertical Line Test also implies that the graph has only one output yy for any input xx. You know that a relation is not a function if there is at least one value of xx that’s related to two different values of yy.
To test for functions, we need to make sure that there’s only one yy-value for every xx-value. Visually, when you look at the graph of a relation, you can see whether every xx-value is related to only one yy-value by using the Vertical Line Test: Any (and every possible) vertical line may intersect (cross) the graph at most once. If some vertical line crosses the graph more than once, then the graph has failed the Vertical Line Test and the relation isn’t a function.
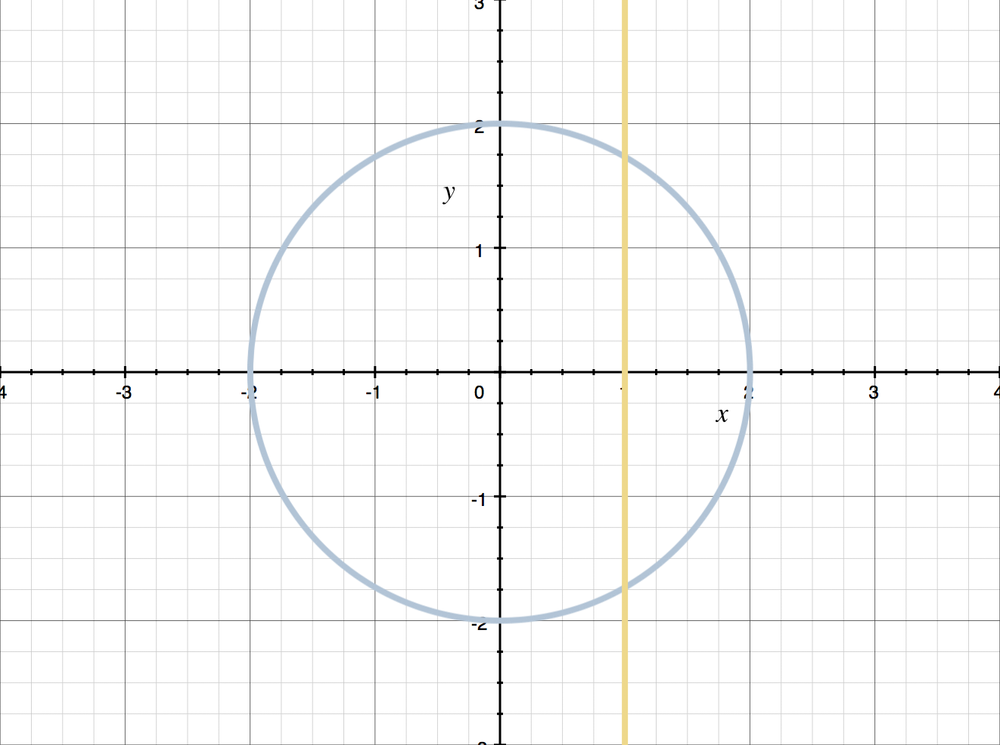
You know that the circle below doesn’t represent a function, because any vertical line you draw at some xx that’s strictly between -2−2 and 22 (not “right at” -2−2 or 22) will cross the graph twice, which causes the graph to fail the Vertical Line Test. In fact, circles can never represent functions, because they never pass the Vertical Line Test.
When does a graph fail the Vertical Line Test?
Example
How many times can a vertical line touch a graph in order to pass the Vertical Line Test?
Every vertical line can only touch a graph once in order for the function to pass the Vertical Line Test. If a graph passes the Vertical Line Test, it’s the graph of a function.
Let’s do an example with another equation.
Example
Determine algebraically whether or not the equation represents a function.
x^2+y^2=1x2+y2=1
Plug in 00 for xx and simplify.
(0)^2+y^2=1(0)2+y2=1
y^2=1y2=1
Now take the square root of each side.
\sqrt{y^2}=\sqrt{1}√y2=√1
y=\pm 1y=±1
Looking at it another way, at x=0x=0 , yy can be both 11 and -1−1 . Since a function can only have one unique output value for yy for any input value of xx, the function fails the Vertical Line Test and is therefore not a function. We’ve now proven with both the graph and with algebra that this circle is not a function.
How Do You Tell If an Equation Is a Vertical Line?
There are many ways to test whether or not your equations are vertical lines. One way to check is to draw a horizontal line through the middle of the graph, so that you have two halves. Then, compare each half with the other. If they’re the same, then the equation should be a straight line.
If the equation isn’t a straight line, then it’s likely that you’ve made some errors. You need to fix these mistakes before you continue. To do this, you’ll want to look at the graph and make sure that you don’t have any extra marks or letters.
You can also use a ruler to help you find the correct answer. This will allow you to measure the distance between the top of the equation and the bottom.
This method works best when you’re dealing with very long equations. However, it won’t work well if your equation is shorter than three points or longer than five.
In addition, there are several online tools that will let you know if an equation is a vertical line. For example, you could try this website: http://www.math-help.com/vertline.html.
How Does a Vertical Line Represent a Function?
A vertical line represents the output of a function. For example, you can write the following expression to determine whether the input number is greater than the given number.
If x > 5 Then
Print “True”
Else
Print “False”
End If
This means that the function returns True when the value of the variable x is greater than five. Otherwise, the function returns False.
You can also use a vertical line to indicate the parameters of a function. This includes the name of the parameter and the type of data that it takes.
For example, here are two functions that have different names but both take one argument:
Function MyFunc(ByVal Parameter As Integer)
MyFunc = Parameter + 1
End Function
Function AnotherFunc()
AnotherFunc = 2
End Function
In this case, the first function has the same name as the second, so you need to include the parentheses when calling the function. The difference between these two examples is that the first function uses ByRef, whereas the second function uses ByVal.