Exponential growth is a concept that describes how something increases in size over time. It has been around since ancient times but was most famously used to describe the population explosion seen during the industrial revolution. However, today we also talk of ‘exponential technology’, which is defined as anything that continues to improve, regardless of its age.
One of the things that set apart an exponential function from other types of mathematical equations is that it does not follow any set rules. This means that there are no fixed numbers and equations, so you can never really predict exactly what will happen. However, this does mean that you don’t need to worry too much about maths if you aren’t good at it!
The best way to differentiate between a simple function (like the example above) and an exponential one is simply by checking whether the variable in the function changes. If the value of x stays constant, then the graph of y=f(x)=ax+b looks very different than when x grows exponentially.
What Is an Exponential Function?
An exponential function can be defined by the following equation:
y = ax^b
Where:
a > 0
x < 1
b >=1
This means that an exponential function increases in value as x gets closer to zero.
If you want to know more about exponential functions, then read on. Here are a few examples of different kinds of exponential functions.
A linear function:
y = MX + c
where:
m>0
c 0
log a is a constant
What are some other ways to describe an exponential function?
The natural logarithm (ln):
ln y = LNA + b*lx
The base e power function:
e^y = exp(a)
When you use an exponential function to solve an algebraic problem, then you’ll need to find the values of a and b. The best way to do this is by using a graphing calculator.
You can also create your exponential function.
What Is Differentiation?
In mathematics, a function is simply a rule that allows you to calculate a number from another number. For example, you can use a function to tell you how many times you have to add 1 to get to 100.
A differentiating function tells you the rate of change of the value of the function. If you know the value of the function at two points, you can figure out where the graph will be. This means that you can determine whether the function increases, decreases, or stays the same.
Differential equations are used to model real-world phenomena such as chemical reactions. You can also use differential equations to describe physical processes like the motion of a ball falling off a cliff.
Differentiation is the process of finding out how fast a function is changing.
For instance, you could differentiate the equation y = x2 to find out that the derivative is 2x. The derivative of f(t) is the slope of the tangent line that touches the curve.
If the function is increasing, then its derivative will always be positive. If it is decreasing, then the derivative will be negative. And if it does not change, then its derivative will equal zero.
Exponential Functions and Their Derivatives
An exponential function is a mathematical expression that shows how an input value changes as the output grows larger. For example, the following equation describes an exponential growth pattern:
In this case, x represents the number of hours after midnight (e.g., midnight). The variable t stands for time. And y represents the amount of money earned at a certain point in time.
If you want to learn more about the basics of exponential functions, then continue reading below.
Here’s another way to understand the concept of an exponential function. Think of a graph. On the horizontal axis, there is a scale that goes from 0 to infinity. Then, on the vertical axis, some values go from negative to positive infinity.
Now imagine that you’re given a graph that looks like the one shown above. In other words, the line on the left side of the graph is zero, and the line on the right side of the graph is infinite.
As you can see, the lines get steeper as they move toward the right. This means that the change in the value of y increases as it moves farther away from zero.
How Do You Find the Differential of an Exponential Function?
If you want to learn how to solve math problems using exponentials, then you need to know how to differentiate them. You might be wondering why you would ever have to take the derivative of an exponential. The answer is that differentiating the exponential gives you a clue about where the value will go.
For example, suppose that you wanted to figure out the total number of seconds that it takes to double your money. Then, the formula for this problem could look like this: 2^(t) = C2.
Now, you can use calculus to find the derivative of the exponential by taking the natural logarithm of both sides of the equation. This means that you should get the following result: ln (C2.
When you do this, you’ll notice that the left side of the equation is equal to zero. Therefore, the right side must also be equal to zero. This means that you can write the final answer as follows: t = -ln 0.
Therefore, you end up with a negative infinity for your time. So, this is a really important lesson about derivatives. When you’re trying to find the rate at which something changes, you always need to start with an exponential function.
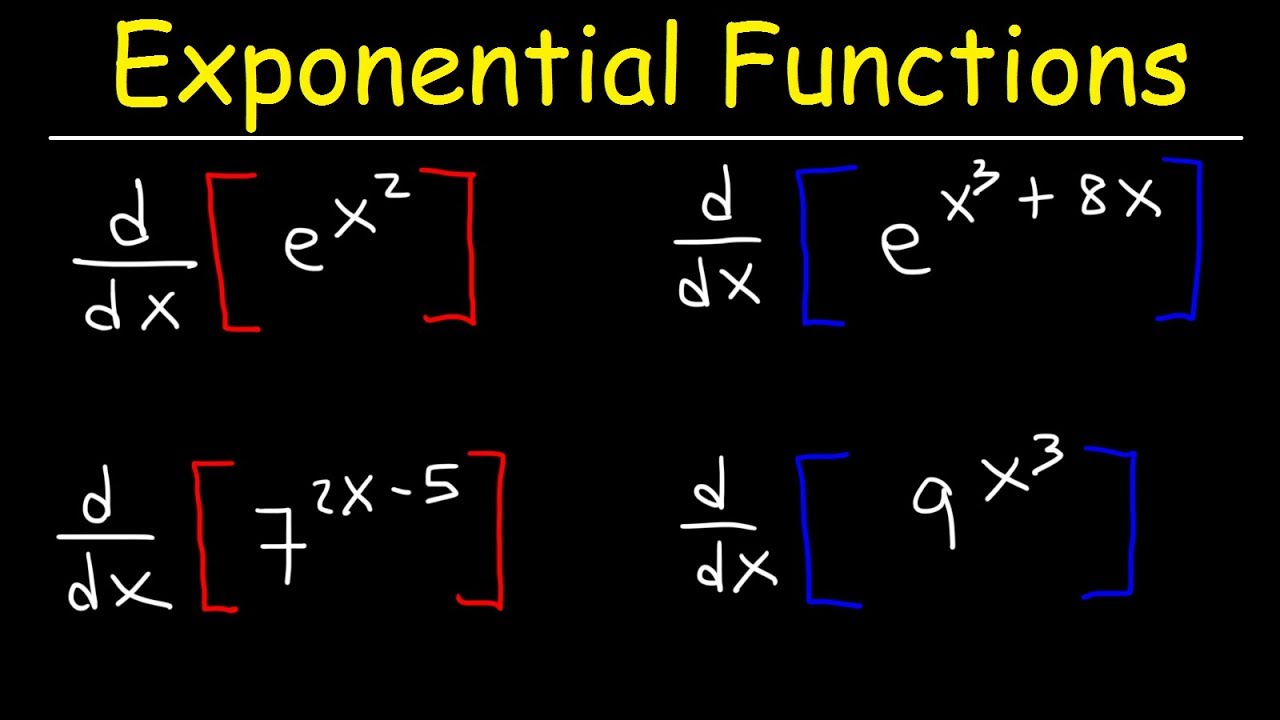
What Is the Exponential Rule in Differentiation?
If you’re taking calculus, then you might be familiar with the concept of exponents. Exponentiation refers to multiplying two numbers together using exponent notation. For example, 3×5 means that you multiply three by five.
Now, here’s where things get interesting. If you have two variables like x and y, then you can use the following equation: (y)^(x). This tells you how much you need to raise one number to another power. For instance, if you want to know how many times you’d have to add 5 to 2 to equal 7, then you would write the answer as follows: ((2 + 5.) ^ (7 – 2.
To understand this better, let’s take a look at a few examples. First of all, consider the problem of finding the value of x. To solve this, you could simply plug in different values for x. So, if you wanted to find the value of x, you would start by writing down some possible answers.
You should also note that when you calculate an exponent, it is always a positive integer. You cannot do anything with negative exponents.
For example, suppose that you wanted to find out what happens when you multiply 4 by (-1.
How to Solve Equation Using Differentiation?
An exponential function is used when the value of a certain variable increases by a specific factor each time. For example, consider a situation where you have $100. If you double that amount every year, you would end up with $200 in two years, $400 in four years, etc.
In mathematics, an exponent is used to represent this type of growth. The symbol for the power function is x^n.
If you want to use a calculator to calculate the answer to an exponential problem, you’ll need to divide the base of the function (in our case, 100. by the exponent of the function. In other words, you will multiply the numerator and denominator by 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, etc.
You can also solve the same problem using logarithms. Logarithmic functions are used to show how many times a number has increased or decreased. You might be familiar with this kind of function because it’s often used in calculating compound interest.
To find out what happens when you increase a variable by a factor of 10 every month, just take the natural log of that number.

