A factor is a number that divides, or goes into, another number exactly.
Another way of saying this is that the other number is a multiple of the factor.
In a fair world, sharing 12 chocolate bars between 4 people leaves each person with 3 chocolate bars.
Divisor is another word for factor. Both words will be used interchangeably through this lesson so you can get more comfortable with them.
The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100.
Factor Pairs of 100
The pairs for 100 are each made from two whole numbers, or integers, that multiply together to make 100.
| Positive Pair | Negative Pair |
| (1, 100) | (-1, -100) |
| (2, 50) | (-2, -50) |
| (4, 25) | (-4, -25) |
| (5, 20) | (-5, -20) |
| (10, 10) | (-10, -10) |
It doesn’t matter which order the multiplication number pairs are given in, because multiplication is commutative.
Commutative means number order can be swapped without making a difference to the answer.
Prime Factors of 100
A prime number can be divided only by 1 and itself.
EXAMPLE:
3 cannot be divided by another number apart from itself.
(3 ÷ 3 = 1)
and
(3 ÷ 1 = 3)
Its only factors are 1 and 3, so it is a prime number.
So from a number’s divisors, at least one MUST be a prime.
For now, 100’s positive factors are 1, 2, 4, 5, 10, 25, 50, and 100
Of these numbers, only 2 and 5 are prime, so those are our prime factors.
How to Find the Factors of 100
A sensible way to find the factors of any number is to find the pairs, by starting with 1, 2, 3, etc., and checking if they divide the number that we want to factorize.
This means that when we find one divisor, we can divide our number by it – which finds another divisor!
That’s how you make a pair.
All factors, apart from square roots, come in pairs like this. For a square number, when dividing it by its square root, we get the same number. For example 100 ÷ 10 = 10.
Fortunately, there are some tricks that allow us to quickly check whether a number is divisible by another.
They’re called divisibility tests.
The table below shows some useful divisibility tests for the numbers 1 to 10, many of which you’ll already know, and whether they give a positive result applied to 100.
Prime Factorization of 100
Returning to the idea from earlier, there is a unique way of writing 100 as a product of only its prime factors. This is called its prime factorization or prime decomposition.
100 can be split into any two of its divisors, then each of those numbers can be split up again into two more. This is repeated until you’re only left with primes which we can’t split up any further.
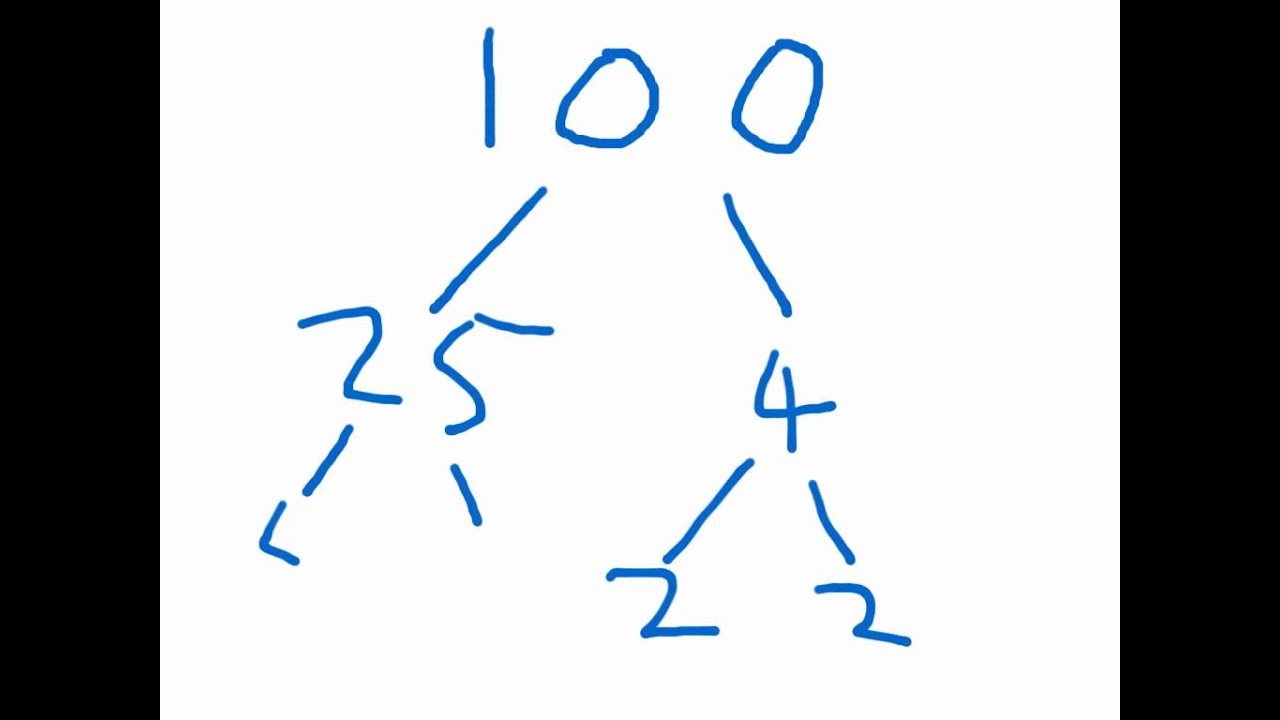
What you end up with is a factor tree, which looks like this:
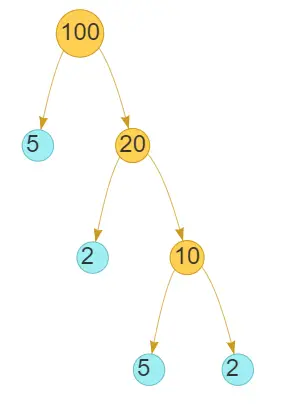
This tree is shown by the equation:
100 = 2 × 2 × 5 × 5
=22 × 52
So, the primes that divide 100 are 2 and 5, and 100 has the unique prime factorization 22 × 52.
All integers have the special property that their prime decomposition is unique – there’s no other way to make 100 using only prime numbers!
We can use the prime decomposition of a number to find all its divisors.
Since any divisor of 100 is made up of some of its prime factors, we just remove some and see what we’re left with:
2 = 2
4 = 2 × 2
5 = 5
10 = 2 × 5
20 = 2 × 2 × 5
25 = 5 × 5
50 = 2 × 5 × 5
100 = 2 × 2 × 5 × 5
What if you don’t care about what the divisors are, just how many there are?
There are 9 different divisors of 100, including 1 and 100.